Building Load Model Forecasting from AMI Data
How to use a model fitted to AMI data to do load forecasting.
In a previous post I described how to fit a discrete linear time-invariant (LTI) dynamic model to AMI or SCADA data from loads. In this post I want to extend that method to the problem of load forecasting. The idea is pretty simple, if we can use an LTI model to predict the next hour, then we can use it to predict an arbitrary number of hours in the future, with the expectation that the further ahead the prediction, the less accurate it is.
Just as a reminder, the LTI model is presented in $z$-domain in the form
\[\frac{P(z)}{T(z)} = \frac{b_0+b_1z^{-1}+\cdots+b_Mz^{-M}}{1+a_1z^{-1}+\cdots+a_Nz^{-N}} \qquad \mathrm{where} ~ N \ge M.\]If we have $K$ samples at the regular interval $t_s$ for $T$ and $P$, then we define the matrix
\[\mathbf{M} = \begin{bmatrix} \mathbf{P}_1 & \cdots & \mathbf{P}_N & \mathbf{T}_0 & \cdots & \mathbf{T}_M \end{bmatrix}\]where
\[\mathbf{T}_k = \begin{bmatrix} T(k) & \cdots & T(K-N+k-1) \end{bmatrix}^\mathrm{T},\] \[\mathbf{P}_k = \begin{bmatrix} P(k) & \cdots & P(K-N+k-1) \end{bmatrix}^\mathrm{T},\]and the vector
\[\mathbf{b} = \begin{bmatrix} \mathbf{P}_0 & \cdots & \mathbf{P}_{-h} \end{bmatrix}.\]where $h$ is the number of hours being forecasted.
We then evaluate $\mathbf{x} = ( \mathbf{M}^T \mathbf{M} )^{-1} \mathbf{M}^T \mathbf{b}$ to obtain the coefficients of the discrete-time transfer function. This is the forecasting model for $h$ hours. The variation we have introduced is essentially the original vector $\mathbf{b}$ copied $h$ times and shifted by one hour for each column.
We will use the same example as the original post, and use this extension to perform a 96 hour load forecast. First, we import the training data:
from pandas import read_csv
data = read_csv('data.csv',index_col=['t'],parse_dates=[0])
print(data)
P T
t
2020-07-01 01:00:00-07:00 3.61584 15.2
2020-07-01 02:00:00-07:00 3.96148 14.2
2020-07-01 03:00:00-07:00 4.60248 13.2
2020-07-01 04:00:00-07:00 5.39665 12.1
2020-07-01 05:00:00-07:00 6.13824 11.1
... ... ...
2020-07-31 20:00:00-07:00 4.82946 16.7
2020-07-31 21:00:00-07:00 4.22882 16.3
2020-07-31 22:00:00-07:00 3.78543 16.0
2020-07-31 23:00:00-07:00 3.59467 15.9
2020-08-01 00:00:00-07:00 3.57846 15.7
[744 rows x 2 columns]
We process the data and solve the model fit problem using a high-order thermal model for the building
from numpy import array, hstack
from numpy.linalg import solve
inputs = ['T']
output = 'P'
K = 25 # model order
H = 24 # forecast hours
X = array(data[inputs])
Y = array(data[[output]])
L = len(Y)
M = hstack([hstack([Y[n:L-K+n-H+1] for n in range(K)]),
hstack([X[n:L-K+n-H+1] for n in range(K+1)])])
Mt = M.transpose()
b = hstack([Y[K+n:L+n-H+1] for n in range(H)])
x = solve(Mt@M,Mt@b)
This gives us $x$ which is the $H$-hour forecasting model based on a $K$-th order dynamic load model.
Validation
To validate the performance of the model, we use data that was not included in the original dataset.
test = pd.read_csv('test.csv',index_col=['t'],parse_dates=[0])
print(test)
P T
t
2020-08-01 01:00:00-07:00 3.55169 15.6
2020-08-01 02:00:00-07:00 3.56701 15.4
2020-08-01 03:00:00-07:00 3.66880 15.3
2020-08-01 04:00:00-07:00 3.98450 15.1
2020-08-01 05:00:00-07:00 4.29065 15.0
... ... ...
2020-08-07 20:00:00-07:00 4.73422 16.1
2020-08-07 21:00:00-07:00 4.48835 15.6
2020-08-07 22:00:00-07:00 4.01017 15.0
2020-08-07 23:00:00-07:00 3.87611 14.4
2020-08-08 00:00:00-07:00 3.89687 13.3
[168 rows x 2 columns]
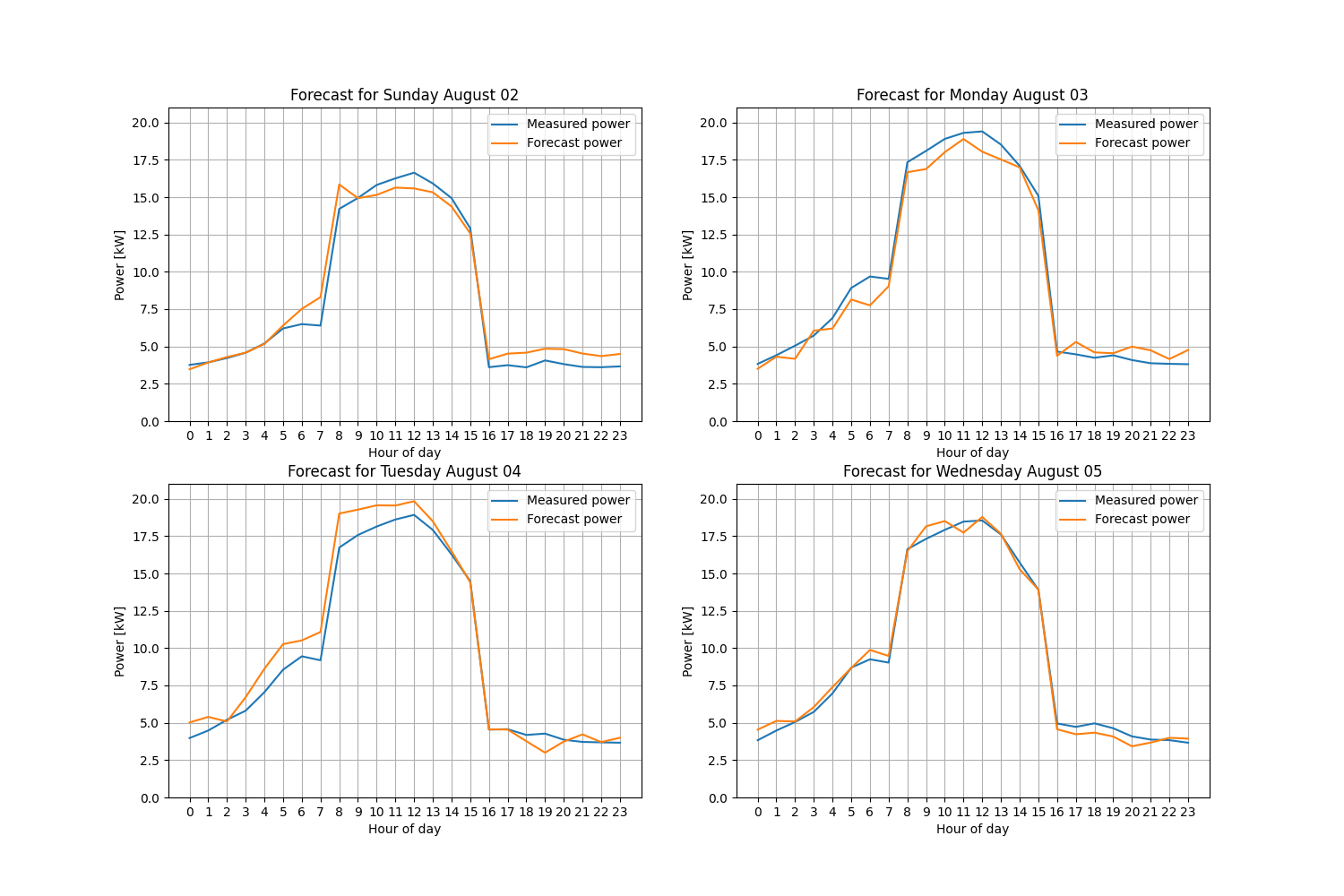
We can use the matrix $M$ for the test data to visualize the performance of the result.
X = array(test[inputs])
Y = array(test[[output]])
L = len(Y)
M = hstack([hstack([Y[n:L-K+n-H+1] for n in range(K)]),
hstack([X[n:L-K+n-H+1] for n in range(K+1)])])
import matplotlib.pyplot as plt
plt.subplots(2,2,figsize=(15,10))
isdst = 1
for t in range(0,96,24):
tt = [str((h.hour-1-isdst)%24) for h in test.index[K+t:K+H+t]]
plt.subplot(2,2,int(t/24)+1)
plt.plot(tt,Y[K+t:K+H+t],label='Measured power')
plt.plot(tt,(M@x)[t].transpose(),label='Forecast power')
plt.grid()
plt.ylim([0,21])
plt.xlabel('Hour of day')
plt.ylabel('Power [kW]')
plt.legend()
plt.title(f"Forecast for {test.index[t+K].strftime('%A %B %d')}")
plt.savefig(f"../../images/2023-02-15-Figure_1.png")
plt.show()
from matplotlib.patches import Rectangle
plt.subplots(2,2,figsize=(15,10))
NL="\n"
for t in range(0,96,24):
err = ((M@x)[t]/Y[K+t:K+H+t].transpose()[0] - 1)*100
tt = [str((h.hour-1-isdst)%24) for h in test.index[K+t:K+H+t]]
plt.subplot(2,2,int(t/24)+1)
plt.gca().add_patch(Rectangle([float(tt[0]),err.mean()-err.std()],23.0,2*err.std(),facecolor='lightgrey'))
plt.plot(tt,err,label=f"Forecast error")
plt.plot([tt[0],tt[-1]],[err.mean(),err.mean()],"--k",label="Mean and stdev")
plt.ylim([-33,33])
plt.grid()
plt.xlabel('Hour of day')
plt.ylabel('Error [%]')
plt.title(test.index[K+1+t].strftime('Forecast error for %A %B %d'))
plt.legend()
plt.savefig(f"../../images/2023-02-15-Figure_2.png")
plt.show()
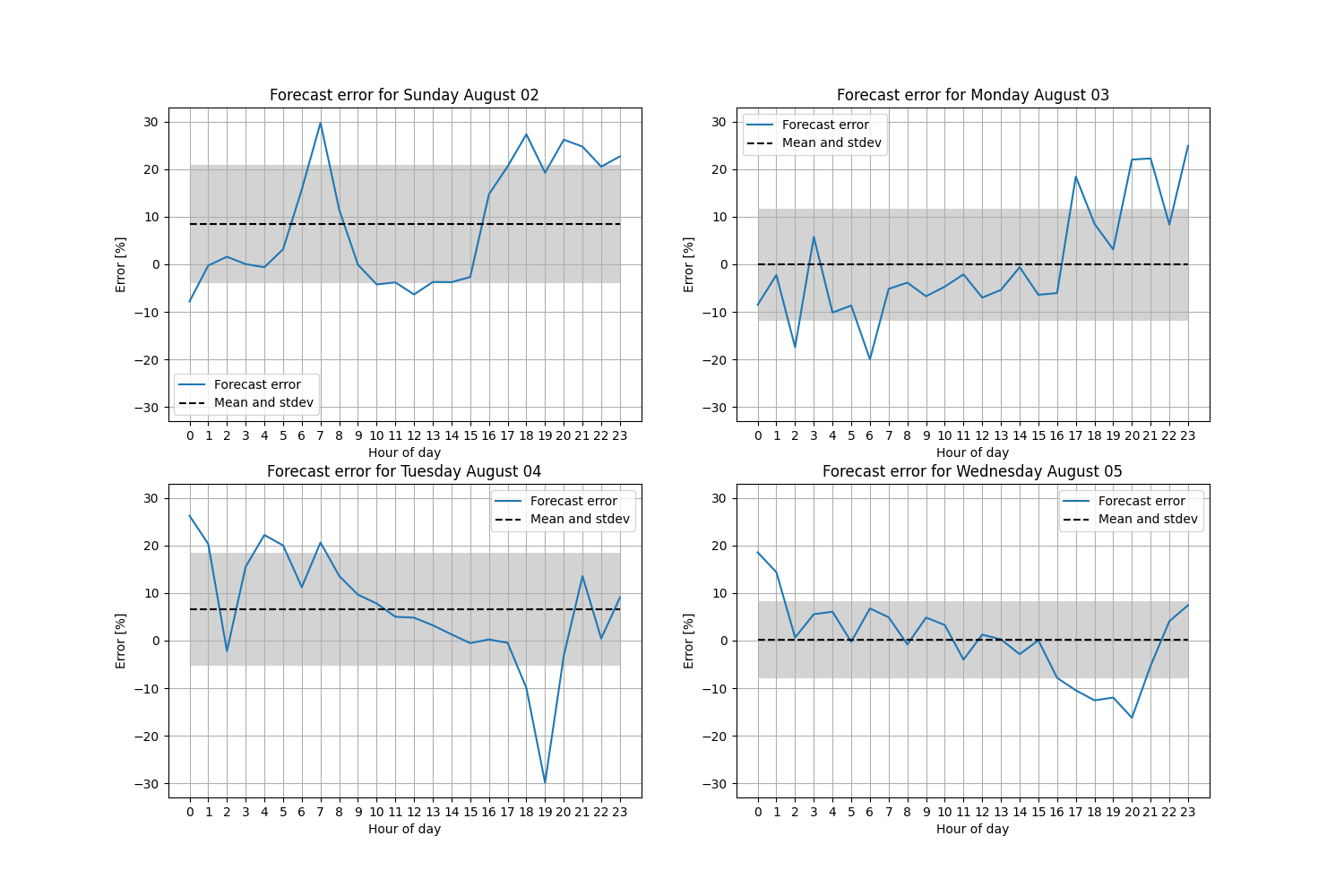
We can see that the forecasts are generally satisfactory for such a simple model, although the forecast for a similar daytype (i.e., weekday, weekend) is better than for a different daytype.